Supervised Regression Model to predict forex price
In this post, I’m going to build a simple supervised regression model to predict tomorrow’s close price of the EUR-USD currencies pair, based on the past close prices and moving averages. In the end, will discuss the error, and show you how the model scores might be misleading.
Let me start with the Yahoo finance package to get the forex data. It is one of the convenient ways to get financial market data. First, install the yfinance package.
pip install yfinance #!pip for Notebook's users
Now, importing the libraries that we need. Here, I used Sklearn, one of the famous libraries for machine learning in Python.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.compose import ColumnTransformer, make_column_transformer
from sklearn.dummy import DummyClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import StandardScaler
plt.rcParams["font.size"] = 16
from datetime import datetime
import yfinance as yf
To get more familiar with how to work with the yfinance package and download financial data, see here and here.
forex_data = yf.download('EURUSD=X', start='2018-01-01', end='2022-09-01')
forex_data.index = pd.to_datetime(forex_data.index)
forex_data.head()
| Open | High | Low | Close | Adj Close | Volume | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2018-01-01 00:00:00+00:00 | 1.200495 | 1.201504 | 1.199904 | 1.200495 | 1.200495 | 0 |
| 2018-01-02 00:00:00+00:00 | 1.201086 | 1.208094 | 1.200855 | 1.201158 | 1.201158 | 0 |
| 2018-01-03 00:00:00+00:00 | 1.206200 | 1.206709 | 1.200495 | 1.206345 | 1.206345 | 0 |
| 2018-01-04 00:00:00+00:00 | 1.201129 | 1.209190 | 1.200495 | 1.201043 | 1.201043 | 0 |
| 2018-01-05 00:00:00+00:00 | 1.206622 | 1.208459 | 1.202154 | 1.206884 | 1.206884 | 0 |
forex_data.isnull().values.any()
False
In the forex data, the Adjusted close price is similar to the close price, so I will drop the corresponding column. Also, the yfinance does not report the trading volume. So, let me drop that column as well.
forex_data = forex_data.drop(['Volume', 'Adj Close'], axis=1)
forex_data.columns
Index(['Open', 'High', 'Low', 'Close'], dtype='object')
Feature engineering
I’m looking for predicting the closing price of the EUR-USD pair on the next day (independent variable) based on some features, such as the prices on the previous days (dependent variable). However, in each row of our data frame, we only have the closing price of each day. What I need to do, is to prepare the data frame in a way that has all the variables I need. That is called feature engineering. To do that, I need to shift the close price column and concatenate the results in a data frame.
close_prices_df = forex_data['Close'].to_frame()
for i in range(1,7):
_closed_lag = forex_data['Close'].to_frame().shift(i)
new_column = "Close_Lag%d" %i
_closed_lag.rename(columns = {'Close':new_column}, inplace = True)
close_prices_df = pd.concat([close_prices_df, _closed_lag], axis =1)
close_prices_df
| Close | Close_Lag1 | Close_Lag2 | Close_Lag3 | Close_Lag4 | Close_Lag5 | Close_Lag6 | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2018-01-01 00:00:00+00:00 | 1.200495 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2018-01-02 00:00:00+00:00 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN | NaN |
| 2018-01-03 00:00:00+00:00 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN |
| 2018-01-04 00:00:00+00:00 | 1.201043 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN | NaN |
| 2018-01-05 00:00:00+00:00 | 1.206884 | 1.201043 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-08-25 00:00:00+01:00 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.017066 |
| 2022-08-26 00:00:00+01:00 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 |
| 2022-08-29 00:00:00+01:00 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 |
| 2022-08-30 00:00:00+01:00 | 1.001402 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 |
| 2022-08-31 00:00:00+01:00 | 1.002506 | 1.001402 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 |
1217 rows × 7 columns
By shifting the data frame, there will be null values that need to be dropped later. Here, I add the moving averages of the close price to the features as well.
def simple_moving_average(data, moving_average_list):
df = pd.DataFrame()
for ma in moving_average_list:
sma_column = f"sma{ma}"
sma = data['Close'].rolling(center=False, window = ma).mean().to_frame(name = sma_column)
df = pd.concat((df, sma), axis=1)
return(df )
sma_df = simple_moving_average(forex_data, [20, 50])
close_sma_prices_df = pd.concat([close_prices_df, sma_df], axis =1)
close_sma_prices_df
| Close | Close_Lag1 | Close_Lag2 | Close_Lag3 | Close_Lag4 | Close_Lag5 | Close_Lag6 | sma20 | sma50 | |
|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||
| 2018-01-01 00:00:00+00:00 | 1.200495 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2018-01-02 00:00:00+00:00 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2018-01-03 00:00:00+00:00 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN | NaN | NaN |
| 2018-01-04 00:00:00+00:00 | 1.201043 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN | NaN |
| 2018-01-05 00:00:00+00:00 | 1.206884 | 1.201043 | 1.206345 | 1.201158 | 1.200495 | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-08-25 00:00:00+01:00 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.017066 | 1.015935 | 1.024769 |
| 2022-08-26 00:00:00+01:00 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.014830 | 1.023618 |
| 2022-08-29 00:00:00+01:00 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.013482 | 1.022513 |
| 2022-08-30 00:00:00+01:00 | 1.001402 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.012245 | 1.021499 |
| 2022-08-31 00:00:00+01:00 | 1.002506 | 1.001402 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.011592 | 1.020484 |
1217 rows × 9 columns
Also, we need to add the close price of the next day to our data frame. This column is our target. We want to predict these target values. To add that, we need to shift the close column of our database backward.
prices_df_final = close_sma_prices_df.assign(Tomorrow_Close = close_sma_prices_df['Close'].shift(-1))
prices_df_final[['Close', 'Tomorrow_Close']].tail()
| Close | Tomorrow_Close | |
|---|---|---|
| Date | ||
| 2022-08-25 00:00:00+01:00 | 0.996910 | 0.997128 |
| 2022-08-26 00:00:00+01:00 | 0.997128 | 0.993868 |
| 2022-08-29 00:00:00+01:00 | 0.993868 | 1.001402 |
| 2022-08-30 00:00:00+01:00 | 1.001402 | 1.002506 |
| 2022-08-31 00:00:00+01:00 | 1.002506 | NaN |
Now, dropping all the null values.
prices_df_final = prices_df_final.dropna()
prices_df_final
| Close | Close_Lag1 | Close_Lag2 | Close_Lag3 | Close_Lag4 | Close_Lag5 | Close_Lag6 | sma20 | sma50 | Tomorrow_Close | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2018-03-09 00:00:00+00:00 | 1.230663 | 1.241465 | 1.241665 | 1.233654 | 1.231542 | 1.227084 | 1.219126 | 1.233603 | 1.226892 | 1.230875 |
| 2018-03-12 00:00:00+00:00 | 1.230875 | 1.230663 | 1.241465 | 1.241665 | 1.233654 | 1.231542 | 1.227084 | 1.233882 | 1.227499 | 1.233958 |
| 2018-03-13 00:00:00+00:00 | 1.233958 | 1.230875 | 1.230663 | 1.241465 | 1.241665 | 1.233654 | 1.231542 | 1.234062 | 1.228155 | 1.239234 |
| 2018-03-14 00:00:00+00:00 | 1.239234 | 1.233958 | 1.230875 | 1.230663 | 1.241465 | 1.241665 | 1.233654 | 1.234255 | 1.228813 | 1.237562 |
| 2018-03-15 00:00:00+00:00 | 1.237562 | 1.239234 | 1.233958 | 1.230875 | 1.230663 | 1.241465 | 1.241665 | 1.233796 | 1.229543 | 1.230921 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-08-24 00:00:00+01:00 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.017066 | 1.016198 | 1.017136 | 1.025744 | 0.996910 |
| 2022-08-25 00:00:00+01:00 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.017066 | 1.015935 | 1.024769 | 0.997128 |
| 2022-08-26 00:00:00+01:00 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.018019 | 1.014830 | 1.023618 | 0.993868 |
| 2022-08-29 00:00:00+01:00 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.008990 | 1.013482 | 1.022513 | 1.001402 |
| 2022-08-30 00:00:00+01:00 | 1.001402 | 0.993868 | 0.997128 | 0.996910 | 0.996691 | 0.993947 | 1.003522 | 1.012245 | 1.021499 | 1.002506 |
1167 rows × 10 columns
Here, I just used some numerical features, derived from prices. In the case of time series data, it is very usual to consider the time and date components in the features. Most of the time series data, have a kind of periodic behavior, and not considering time and date, will not catch those behaviors. However, I think specifically for the forex data, that is not a good idea! later, I will write about my reasons in a separate blog post.
train_test split
The common way of evaluating and verifying the performance of a machine learning model before using is to test it on a section of the data. What is important here is the section that we consider for testing the model, must not be part of the training of the model. To be sure that this will not happen unwillingly, the SKlearn has a special function called train_test_split. With the use of this function, we can split our data to train and test sections. However, the time series are different stories! We have a series of events that happen over time. If we want to predict something, we are not allowed to know anything from the future! The train_test_split samples randomly from data. We do not want to train our model based on data that came after our test data! The simplest way here is to separate the data based on a specific date. Before that date, is our training data, and after that is our test data.
prices_df_final.isnull().any().values
array([False, False, False, False, False, False, False, False, False,
False])
n_train = int(0.8 * len(prices_df_final))
train_df = prices_df_final.iloc[:n_train, :]
test_df = prices_df_final.iloc[n_train:, :]
print(train_df.shape, test_df.shape)
(933, 10) (234, 10)
I separated my data based on its length. About 80% of the data is going to be used for traing our model, and 20% for testing it.
print(train_df.index.max(), test_df.index.min())
2021-10-06 00:00:00+01:00 2021-10-07 00:00:00+01:00
Preprocessing
Here, I’m going to define the preprocessing steps, to prepare data to fit the models.
prices_df_final.columns
Index(['Close', 'Close_Lag1', 'Close_Lag2', 'Close_Lag3', 'Close_Lag4',
'Close_Lag5', 'Close_Lag6', 'sma20', 'sma50', 'Tomorrow_Close'],
dtype='object')
numerical_features = [
'Close', 'Close_Lag1', 'Close_Lag2', 'Close_Lag3', 'Close_Lag4',
'Close_Lag5', 'Close_Lag6', 'sma20', 'sma50',
]
drop_features = [
'Tomorrow_Close',
]
def preprocess_features(
train_df,
test_df,
numerical_features,
drop_features,
):
numeric_transfer = StandardScaler()
preprocessor = make_column_transformer(
(numeric_transfer, numerical_features),
("drop", drop_features),
)
preprocessor.fit(train_df)
new_columns = numerical_features
X_train = pd.DataFrame(
preprocessor.transform(train_df), index=train_df.index, columns=new_columns
)
X_test = pd.DataFrame(
preprocessor.transform(test_df), index=test_df.index, columns=new_columns
)
y_train = train_df['Tomorrow_Close']
y_test = test_df['Tomorrow_Close']
return X_train, X_test, y_train, y_test, preprocessor
X_train, X_test, y_train, y_test, preprocessor = preprocess_features(
train_df,
test_df,
numerical_features,
drop_features,
)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
(933, 9) (234, 9) (933,) (234,)
The model will train based on X_train and y_train, and evaluate on X_test and y_test. The y_test is our target, and we are going to make our prediction as close as possible to it.
Supervised Learing
def model_evaluation(X_train, X_test, y_train, y_test, regressor_model):
regressor_model.fit(X_train, y_train)
print("Train-set R^2: {:.5f}".format(regressor_model.score(X_train, y_train)))
print("Test-set R^2: {:.5f}".format(regressor_model.score(X_test, y_test)))
y_pred = regressor_model.predict(X_test)
y_pred_train = regressor_model.predict(X_train)
plt.figure(figsize=(10, 3))
strt_day = 200
plt.plot(range(len(y_train) - strt_day, n_train), y_train.iloc[len(y_train) - strt_day:], label="train")
plt.plot(range(len(y_train) - strt_day, n_train), y_pred_train[len(y_train) - strt_day:], "--", label="prediction train")
plt.plot(range(n_train, len(y_test) + n_train), y_test, "-", label="test")
plt.plot(
range(n_train, len(y_test) + n_train), y_pred, "--", label="prediction test"
)
plt.legend(loc=(1.01, 0))
plt.xlabel("Trading day")
plt.ylabel("Close Price")
DummyRegressor:
Let’s start with a dummy reggression model, a buildt-in package in sklearn. This is a good prectice to compare our model to a dummy model, to be sure that it makes a meaningful results (not similar to a dummy model!)
from sklearn.dummy import DummyRegressor
dummy = DummyRegressor()
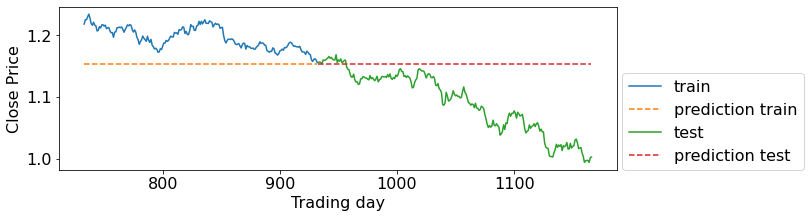
model_evaluation(X_train, X_test, y_train, y_test, dummy)
Train-set R^2: 0.00000
Test-set R^2: -1.57690
Random Forest Regressor:
Do not use tree-based models with time series data! Especially, when you are dealing with time and dates as the features in your model. Here, I did not include the date-time in my data, so let’s see the performance of the random forest regressor.
from sklearn.ensemble import RandomForestRegressor
RFRegressor = RandomForestRegressor(n_estimators=100, random_state=0)
model_evaluation(X_train, X_test, y_train, y_test, RFRegressor)
Train-set R^2: 0.99802
Test-set R^2: 0.50661
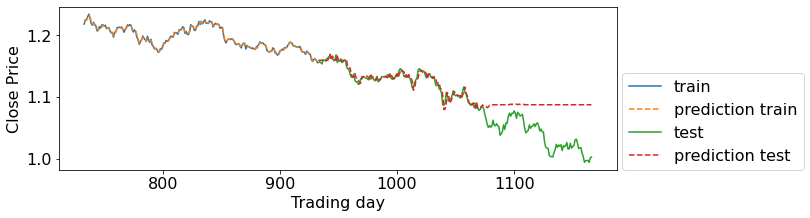
This is a typical result you might get when using a tree-based model with time series data!
Support vector machine with RBF kernel:
Let me try another famous regression model.
from sklearn.svm import SVR
svm = SVR(kernel="rbf", C= 1, gamma=0.002, epsilon=0.001)
model_evaluation(X_train, X_test, y_train, y_test, svm)
Train-set R^2: 0.98759
Test-set R^2: 0.95122
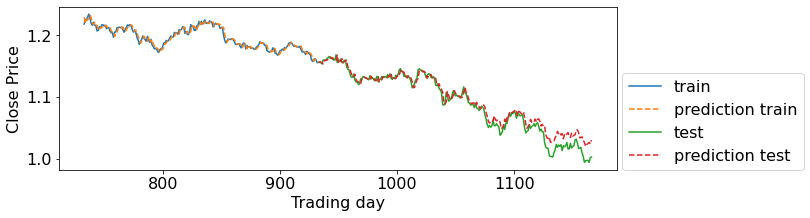
I might get better results if I tune the hyperparameters of the model, but I prefer to leave it as it is and check another model!
Ridge:
Ridge is a linear regression model in the sklearn package.
from sklearn.linear_model import Ridge
lr_ridge = Ridge(alpha = 1)
model_evaluation(X_train, X_test, y_train, y_test, lr_ridge)
Train-set R^2: 0.98762
Test-set R^2: 0.98675
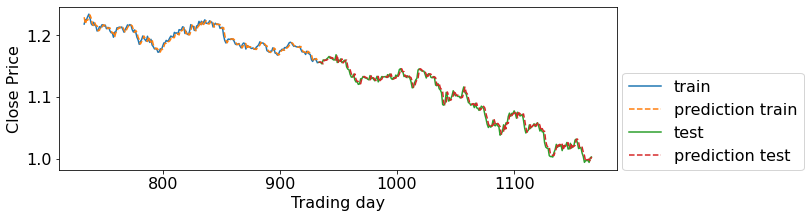
The model R-squared score is more than 0.98 for our test data! Isn’t that promising?! Well, actually not! Interpreting R-squared here is a bit tricky! let me calculate the Mean Absolute Error. That will give us a better insight.
def mae(true, pred): #mean absolute error
return np.mean(np.abs((pred - true)))
y_pred = lr_ridge.predict(X_test)
ridge_scores = {"R^2": [lr_ridge.score(X_test, y_test)],
"MAE": [mae(y_test, y_pred)]
}
pd.DataFrame.from_dict(ridge_scores)
| R^2 | MAE | |
|---|---|---|
| 0 | 0.986752 | 0.004311 |
The Mean Absolute Error is 0.0043! It means on average, your prediction is off by 0.0043. At the first glance, it seems very low! But, for knowing what this number shows, you need to know a little bit more about forex trading! Forex trader calculate their gain and loss based on a unit, called Pip! One pip is a change in the value of the currencies pair by 0.0001 (It might be different for some currencies pairs). So, 0.0043 means 43 pip error! If you trade one “standard lot” (which is another trading term), a 43 pip error means $430! It is a huge error for each trade! Let me plot fewer trading days to see what is going on!
td_start = 0
td_end = 20
plt.figure(figsize=(10, 3))
plt.plot(range(td_start, td_end), y_test[td_start:td_end], 'b', label='tomorrow Close')
plt.plot(range(td_start, td_end), y_pred[td_start:td_end], 'r', label='prediction Close')
plt.plot(range(td_start, td_end), test_df['Close'][td_start:td_end], 'g', label='today Close')
plt.xticks(rotation="vertical")
plt.legend();
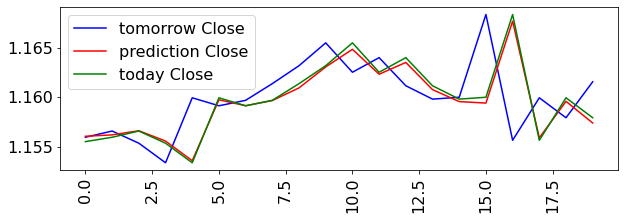
As can be seen, the model predicted the close price of the other day, as it is for today! The R-squared score shows a tremendous outcome for our model, just because these two prices are very close to each other!